Topic 2 Review of Factoring

2.1 Can You Beat a Calculator

Do you know a faster way to find the values?

Find the value of the polynomial $2 x^{3} - 98 x$ when $x = - 7$ .
Find the value of the polynomial $x^{2} - 9 x - 22$ when $x = 11$ .
Find the value of the polynomial $x^{3} - 2 x^{2} - 9 x + 18$ when $x = - 3$ .
Find the value of $16^{2} - 14^{2}$ .

2.2 Factor by Removing the GCF

The greatest common factor (GCF) of two terms is a polynomial with the greatest coefficient and of the highest possible degree that divides each term.

To factor a polynomial is to express the polynomial as a product of polynomials of lower degrees. The first and the easiest step is to factor out the GCF of all terms.

Example 2.1 Factor $4 x^{3} y - 8 x^{2} y^{2} + 12 x^{3} y^{3}$ .

Solution.

Find the GCF of all terms.
The GCF of $4 x^{3} y$ , $- 8 x^{2} y^{2}$ and $12 x^{4} y^{3}$ is $4 x^{2} y$ .
Write each term as the product of the GCF and the remaining factor.
$4 x^{3} y = (4 x^{2} y) \cdot x$ , $- 8 x^{2} y^{2} = (4 x^{2} y) \cdot (- 2 y)$ , and $12 x^{4} y^{3} = (4 x^{2} y) (3 x y^{2})$ .
Factor out the GCF from each term.
$4 x^{3} y - 8 x^{2} y^{2} + 12 x^{3} y^{3} = 4 x^{2} y \cdot (x - 2 y + 3 x y^{2})$ .

2.3 Factor by Grouping

For a four-term polynomial, in general, we will group them into two groups and factor out the GCF for each group and then factor further.

Example 2.2 Factor $2 x^{2} - 6 x y + x z - 3 y z$ .

Solution.

For a polynomial with four terms, one can normally try the grouping method.

Group the first two terms and the last two terms. $\begin{aligned} 2 x^{2} - 6 x y + x z - 3 y z \\ = & (2 x^{2} - 6 x y) + (x z - 3 y z) \end{aligned}$
Factor out the GCF from each group.
$\begin{aligned} = & 2 x (x - 3 y) + z (x - 3 y) \end{aligned}$
Factor out the binomial GCF. $\begin{aligned} = & (x - 3 y) (2 x + z) . \end{aligned}$

Example 2.3 Factor $a x + 4 b - 2 a - 2 b x$ .

Solution.

Group the first term with the third term and group the second term with the last term. $\begin{aligned} a x + 4 b - 2 a - 2 b x \\ = & (a x - 2 a) + (- 2 b x + 4 b) \end{aligned}$
Factor out the GCF from each group. $\begin{aligned} = & a (x - 2) + (- 2 b) (x - 2) \end{aligned}$
Factor out the binomial GCF. $\begin{aligned} = & (x - 2) (a - 2 b) . \end{aligned}$

Guess and check.

Once you factored one group, you may expect that the other group has the same binomial factor so that factoring may be continued.

2.4 Factor Difference of Powers

Factoring is closely related to solving polynomial equations. If a polynomial equation $p (x) = 0$ has a solution $r$ , then $p (x)$ has a factor $x - r$ . For example, $x^{n} - r^{n} = 0$ has a solution $x = r$ . So the difference $x^{n} - r^{n}$ has a factor $(x - r)$ . Using long division or by induction, we obtain the following equality.

Difference of $n$ -th powers

$a^{n} - b^{n} = (a - b) (a^{n - 1} + a^{n - 2} b + \dots + a b^{n - 2} + b^{n - 1})$

In particular,

$a^{2} - b^{2} = (a - b) (a + b) .$

Example 2.4 Factor $25 x^{2} - 16$ .

Solution.

Recognize the binomial as a difference of squares. $\begin{aligned} 25 x^{2} - 16 \\ = & (5 x)^{2} - 4^{2} \end{aligned}$
Apply the formula. $\begin{aligned} = & (5 x - 4) (5 x + 4) . \end{aligned}$

Example 2.5 Factor $32 x^{3} y - 2 x y^{5}$ completely.

Solution.

$\begin{aligned} 32 x^{3} y - 2 x y^{3} = & 2 x y (16 x^{2} - y^{4}) \\ = & 2 x y ((4 x)^{2} - (y^{2})^{2}) \\ = & 2 x y (4 x + y^{2}) (4 x - y^{2}) . \end{aligned}$

2.5 Factor Trinomials

If a trinomial $a x^{2} + b x + c$ , $A \neq 0$ , can be factored, then it can be expressed as a product of two binomials:
$a x^{2} + b x + c = (m x + n) (p x + q) .$ By simplify the product using the FOIL method and comparing coefficients, we observe that
$a = \underset{F}{\underset{⏟}{m n}} b = \underset{O}{\underset{⏟}{m q}} \underset{+}{\underset{}{+}} \underset{I}{\underset{⏟}{n p}} c = \underset{F}{\underset{⏟}{n q}}$

A trinomial $a x^{2} + b x + c$ is also called a quadratic polynomial. The function defined by $f (x) = a x^{2} + b x + c$ is called a quadratic function.

Trial and error.

The observation suggests to use trial and error to find the undetermined coefficients $m$ , $n$ , $p$ , and $q$ from factors of $a$ and $c$ such that the sum of cross products $m q + n p$ is $b$ . A diagram as shown in the following examples will be helpful to check a trial.

Example 2.6 Factor $x^{2} + 6 x + 8$ .

Solution. One may factor the trinomial in the following way.

Factor $a = 1$ : $1 = 1 \cdot 1.$
Factor $c = 8$ : $8 = 1 \cdot 8 = 2 \cdot 4.$
Choose a proper combination of pairs of factors and check if the sum of cross product equals $b = 6$ : $1 \cdot 4 + 1 \cdot 2 = 6.$
This step can be checked easily using the following diagram.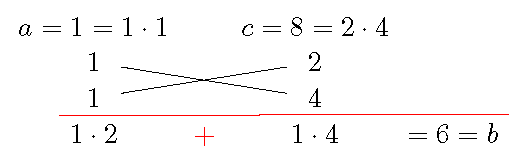
Factor the trinomial $x^{2} + 6 x + 8 = (x + 2) (x + 4) .$

Example 2.7 Factor $2 x^{2} + 5 x - 3$ .

Solution. One may factor the trinomial in the following way.

Factor $a = 2$ : $1 = 1 \cdot 2.$
Factor $c = - 3$ : $- 3 = 1 \cdot (- 3) = (- 1) \cdot 3.$
Choose a proper combination of pairs of factors and if the sum of cross products equals $b = 5$ :
$2 \cdot 3 + 1 \cdot (- 1) = 5.$
This step can be checked easily using the following diagram.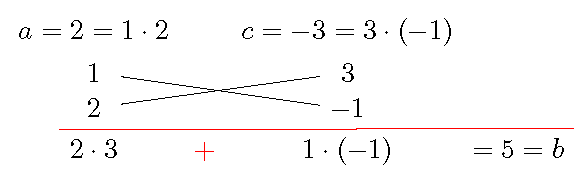
Factor the trinomial $2 x^{2} + 5 x - 3 = (x + 3) (2 x - 1) .$

Use Auxiliary Problem.

Some higher degree polynomials may be rewrite as a trinomial after a substitution. Factoring the trinomial helps factor the polynomial.

Example 2.8 Factor the trinomial completely.

$4 x^{4} - x^{2} - 3$

Solution. One idea is to use a substitute.

Let $x^{2} = y$ . Then $4 x^{4} - x^{2} - 3 = 4 y^{2} - y - 3$ .
Factor the trinomial in $y$ : $4 y^{2} - y - 3 = (4 y + 3) (y - 1)$ .
Replace $y$ by $x^{2}$ and factor further. $\begin{aligned} 4 x^{4} - x^{2} - 3 & = 4 y^{2} - y - 3 \\ = (4 y + 3) (y - 1) \\ = (4 x^{2} + 3) (x^{2} - 1) \\ = (4 x^{2} + 3) (x - 1) (x + 1) . \end{aligned}$

2.6 Practice

Problem 2.1 Factor out the GCF.

$18 x^{2} y^{2} - 12 x y^{3} - 6 x^{3} y^{4}$
$5 x (x - 7) + 3 y (x - 7)$
$- 2 a^{2} (x + y) + 3 a (x + y)$

Problem 2.2 Factor by grouping.

$12 x y - 10 y + 18 x - 15$
$12 a c - 18 b c - 10 a d + 15 b d$
$5 a x - 4 b x - 5 a y + 4 b y$

Problem 2.3 Factor completely.

$25 x^{2} - 4$
$8 x^{3} - 2 x$
$25 x y^{2} + x$

Problem 2.4 Factor completely.

$3 x^{3} + 6 x^{2} - 12 x - 24$
$x^{4} + 3 x^{3} - 4 x^{2} - 12 x$

Problem 2.5 Factor the trinomial.

$x^{2} + 4 x + 3$
$x^{2} + 6 x - 7$
$x^{2} - 3 x - 10$

Problem 2.6 Factor the trinomial.

$5 x^{2} + 7 x + 2$
$2 x^{2} + 5 x - 12$
$3 x^{2} - 10 x - 8$

Problem 2.7 Factor completely into polynomials with integer coefficients.

$x^{3} - 5 x^{2} + 6 x$
$4 x^{4} - 12 x^{2} + 5$
$2 x^{3} y - 9 x^{2} y^{2} - 5 x y^{3}$

Problem 2.8 Each of trinomial below has a factor in the table. Match the letter on the left of a factor with a the number on the left a trinomial to decipher the following quotation.

“ $\frac{}{13}$ $\frac{}{10 2 9 15}$ , $\frac{}{9 5 14}$ $\frac{}{13}$ $\frac{}{4 3 15 7 2 1}$ ; $\frac{}{13}$ $\frac{}{11 2 2}$ , $\frac{}{9 5 14}$ $\frac{}{13}$ $\frac{}{8 5 3 6}$ ; $\frac{}{13}$ $\frac{}{14 3}$ , $\frac{}{9 5 14}$ $\frac{}{13}$ $\frac{}{12 5 14 2 15 11 1 9 5 14}$ .”

A: $3 x - 2$	B: $2 x + 1$	C: $x + 6$	D: $x + 7$	E: $2 x - 1$	F: $3 x - 1$	G: $x + 10$
H: $x - 8$	I: $2 x + 9$	J: $x - 1$	K: $x + 3$	L: $2 x - 5$	M: $x + 5$	N: $x - 7$
O: $x - 13$	P: $5 x - 3$	Q: $4 x - 11$	R: $x - 9$	S: $2 x + 3$	T: $x + 4$	U: $7 x + 1$
V: $3 x + 5$	W: $3 x + 4$	X: $8 x + 3$	Y: $x - 14$	Z: $5 x - 6$

$x^{2} - 2 x - 24$
$6 x^{2} + x - 2$
$x^{2} - 16 x + 39$
$6 x^{2} + 13 x - 5$
$x^{2} - 5 x - 14$
$3 x^{2} - 5 x - 12$
$x^{2} - x - 110$
$x^{2} - 9$
$- 3 x^{2} + 11 x - 6$
$x^{2} - 10 x + 16$
$- 2 x^{2} + 5 x + 12$
$42 x^{2} - x - 1$
$- 2 x^{2} - 3 x + 27$
$x^{2} + 14 x + 49$
$x^{2} - 81$