Topic 17 Logarithmic Functions

17.1 Estimate the Number of Digits

Can you estimate the number of digits in the integer part of the number 2^{15}\times \sqrt{2020}\div 2021?

17.2 Definition and Graphs of Logarithmic Function

For x>0, b>0 and b\neq 1, there is a unique number y satisfying the equation b^y=x. We denote the unique number y by \log_bx, read as logarithm to the base b of x. In other words, the defining relation between exponentiation and logarithm is y=\log_bx \quad\text{if and only if} \quad b^y=x. The function f(x)=\log_bx is called the logarithmic function f of x with the base b.

Graphs of logarithmic functions:

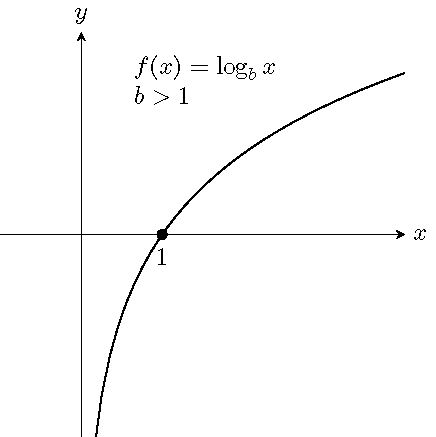
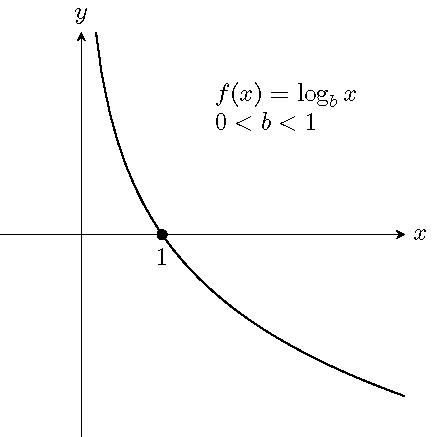
17.3 Common Logarithms and Natural Logarithms

A logarithmic function f(x) with base 10 is called the common logarithmic function and denoted by f(x)=\log x.

A logarithmic function f(x) with base the natural number e is called the natural logarithmic function and denoted by f(x)=\ln x.

17.4 Basic Properties of Logarithms

When b>0 and b\neq 1, and x>0, we have

  1. b^{\log_bx}=x.
  2. \log_b(b^x)=x.
  3. \log_bb=1 and \log_b1=0.

Example 17.1 Convert between exponential and logarithmic forms.

  1. \log x=\frac{1}{2}
  2. 3^{2x-1}=5

Solution.

When converting between exponential and logarithmic forms, we move the base from one side to the other side, then add or drop the log sign.

  1. Move the base 10 to the right side and drop the log from the left: x=10^{\frac{1}{2}}
  2. Move the 3 to the right and add log the the right: 2x-1=\log_35

Example 17.2 Evaluate the logarithms.

  1. \log_42
  2. 10^{\log(\frac{1}{2})}
  3. \log_5(e^0)

Solution.

The key is to rewrite the log and the power so that they have the same base.

  1. \log_42= \log_44^{\frac{1}{2}}=\frac{1}{2}.
  2. 10^{\log\frac{1}{2}}=10^{\log_{10}\frac{1}{2}}=\frac12
  3. \log_5(e^0)=\log_51=0

Example 17.3 Find the domain of the function f(x)=\ln(2-3x).

Solution.

The function has a real output if 2-3x>0. Solving the inequality, we get x<\frac{2}{3}. So the domain of the function is (-\infty, \frac{2}{3}).

17.5 Properties of Logarithms

For M>0, N>0, b>0 and b\neq 1, we have

  1. (The product rule) \log_b(MN)=\log_bM+\log_bN
  2. (The quotient rule) \log_b(\frac MN)=\log_bM-\log_bN.
  3. (The power rule) \log_b(M^p)=p\log_bM, where p is any real number.
  4. (The change-of-base property) \log_bM=\dfrac{\log_aM}{\log_ab}, where a>0 and a\neq 1. In particular, \log_bM=\dfrac{\log M}{\log b} \quad\text{and}\quad \log_bM=\dfrac{\ln M}{\ln b}.

Example 17.4 Expand and simplify the logarithm \log_2\left(\frac{8\sqrt{y}}{x^3}\right).

Solution.

\begin{aligned} \log_2\left(\frac{8\sqrt{y}}{x^3}\right)&=\log_2(8\sqrt{y})-\log_2(x^3)\\ &=\log_28+\log_2(y^{\frac{1}{2}})-3\log_2x\\ &=3+\frac{1}{2}\log_2y-3\log_2x. \end{aligned}

Example 17.5 Write the expression 2\ln(x-1)-\ln(x^2+1) as a single logarithm.

Solution.

2\ln(x-1)-\ln(x^2+1)=\ln((x-1)^2)-\ln(x^2+1)=\ln\left(\frac{(x-1)^2}{x^2+1}\right).

Example 17.6 Evaluate the logarithm \log_34 and round it to the nearest tenth.

Solution.

On most scientific calculator, there are only the common logarithmic function LOG and the natural logarithmic function LN. To evaluate a logarithm based on a general number, we use the change-of-base property. In this case, the value of \log_34 is \log_34=\frac{\log4}{\log3}\approx 1.3.

Example 17.7 Simplify the logarithmic expression \log_2(x^{\log 3})\log_32.

Solution.

\log_2(x^{\ln 3})\log_32 =(\ln 3\log_2x)\log_32=\ln3\left(\frac{\ln x}{\ln 2}\right)\left(\frac{\ln 2}{\ln 3}\right)=\ln x.

17.6 Practice

Problem 17.1 Write each equation into equivalent exponential form.

  1. \log_37=y
  2. 3=\log_b64
  3. \log x=y
  4. \ln(x-1)=c

Problem 17.2 Write each equation into equivalent logarithmic form.

  1. 7^x=10
  2. b^5=2
  3. e^{2y-1}=x
  4. 10^x=c^2+1

Problem 17.3 Evaluate.

  1. \log_216
  2. \log_93
  3. \log 10
  4. \ln 1

Problem 17.4 Evaluate.

  1. e^{\ln 2}
  2. \log 10^{\frac13}
  3. \ln(\sqrt{e})
  4. \log_2(\frac12)

Problem 17.5 Find the domain of the function f(x)=\log(x-5). Write in interval notation.

Problem 17.6 Sketch the graph of each function and find its range.

  1. f(x)=\log_2x
  2. f(x)=\log_{\frac12} x

Problem 17.7 Expand the logarithm and simplify.

  1. \log(100x)
  2. \ln\left(\frac{10}{e^2}\right)
  3. \log_b(\sqrt[3]{x})
  4. \log_7(\frac{x^2\sqrt{y}}{z})

Problem 17.8 Expand the logarithm and simplify.

  1. \log_b\sqrt{\frac{x^2y}{5}}
  2. \ln(\sqrt[3]{(x^2+1)y^{-2}})
  3. \log(x\sqrt{10x}-\sqrt{10x})

Problem 17.9 Write as a single logarithm.

  1. \frac13\log x +\log y
  2. \frac12\ln(x^2+1)-2\ln x
  3. \frac13\log_2 x - 3\log_2(x+1)+1

Problem 17.10 Write as a single logarithm.

  1. 2\log(2x+1)-\frac12\log x
  2. 3\ln x - 5\ln y + \frac{1}{2}\ln z
  3. 3\log_3 x-2\log_3(1-x)+\frac13\log_3 (x^2+1).

Problem 17.11 Evaluate the logarithm and round it to the nearest hundredth.

  1. \log_2 10
  2. \log_3 5
  3. \dfrac{1}{\log_52}
  4. \log_45-\log_29

Problem 17.12 Simplify the logarithmic expression \frac{\log_3(x^2)\log_y\sqrt{3}}{\log x}.