Topic 16 Exponential Functions

16.1 Half-life

Half-life is the time required for a quantity to reduce to half of its initial value.

A certain pesticide is used against insects. The half-life of the pesticide is about 12 days. After a month how much would left if the initial amount of the pesticide is 10 g? Can you write a function for the remaining quantity of the pesticide after $t$ days?

More examples on exponential functions can be found on http://passyworldofmathematics.com/exponents-in-the-real-world/.

16.2 Definition and Graphs of Exponential Functions

Let $b$ be a positive number other than $1$ (i.e. $b>0$ and $b\ne 1$). The exponential function $f$ of $x$ with the base $b$ is defined as $$f\left(x\right)=b^x\text{or}y=b^x.$$

Graphs of exponential functions:

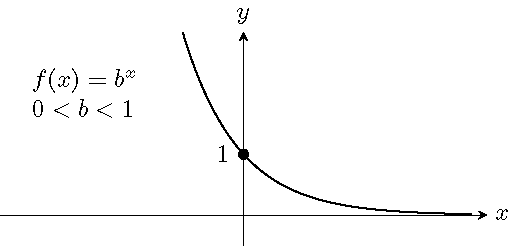
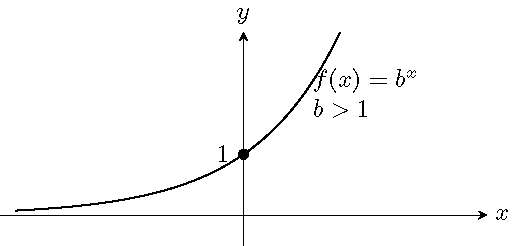
The exponential function $f\left(x\right)=b^x$ is a one-to-one function: any vertical line or any horizontal line crosses the graph at most once. Equivalently, the equation $b^x=c$ has at most one solution for any real number $c$.

16.3 The Natural Number $e$

The natural number $e$ is the number to which the quantity ${(1+\frac{1}{n})}^n$ approaches as $n$ takes on increasingly large values. Approximately, $e\approx 2.718281827$.

16.4 Compound Interests

After $t$ years, the balance $A$ in an account with a principal $P$ and annual interest rate $r$ is given by the following formulas:

1. For $n$ compounding periods per year: $A=P{(1+\frac{r}{n})}^{nt}$.
2. For compounding continuously: $A=P{e}^{rt}$.

Example 16.1 A sum of $\$10,000$ is invested at an annual rate of $8\%$, Find the balance, to the nearest hundredth dollar, in the account after $5$ years if the interest is compounded

1. monthly,
2. quarterly,
3. semiannually,
4. continuous.

Solution.

1. Find values of $P$, $r$, $t$ and $n$. In this case, $P=10,000$, $r=8\%=0.08$, $t=5$ and $n$ depends compounding.
2. Plug the values in the formula and calculate.
3. Monthly’’ means $n=12$. Then $$A=10000{(1+\frac{0.08}{12})}^{5\cdot 12}\approx \mathrm{14898.46.}$$
4. Quarterly’’ means $n=4$. Then $$A=10000{(1+\frac{0.08}{4})}^{5\cdot 4}\approx \mathrm{14859.47.}$$
5. semiannually’’ means $n=2$. Then $$A=10000{(1+\frac{0.08}{2})}^{5\cdot 2}\approx \mathrm{14802.44.}$$
6. For continuously compounded interest, we have $$A=10000e^{0.08\cdot 5}\approx \mathrm{14918.25.}$$

In the compounded investment module, the $\frac{r}{n}$ is an approximation of the period interest rate. Indeed, if the period rate $p$ satisfies the equation $(1+p{)}^n=1+r$, or equivalently $p=\sqrt[n]{n1+r}-1$. Using the formula $(1+x{)}^n=1+nx+\frac{n(n-1)}{2}{x}^2+\cdots +x^n$, one may approximately replace $1+r$ by $(1+\frac{r}{n})$ and obtain the approximation $p\approx \frac{r}{n}$.

Example 16.2 The population of a country was about 0.78 billion in the year 2015, with an annual growth rate of about 0.4%. The predicted population is $P\left(t\right)=0.78(1.004{)}^t$ billions after $t$ years since 2015. To the nearest thousandth of a billion, what will the predicted population of the country be in 2030?

Solution.

The population is approximately $$P\left(15\right)=0.78(1.004{)}^{15}\approx 0.828\text{billions}.$$

16.5 Practice

Problem 16.1 The value of a car is depreciating according to the formula: $V=25000(3.2{)}^{-0.05x}$, where $x$ is the age of the car in years. Find the value of the car, to the nearest dollar, when it is five years old.

Problem 16.2 A sum of $20,000 is invested at an annual rate of 5.5%, Find the balance, to the nearest dollar, in the account after 5 years subject to

1. monthly compounding,
2. continuously compounding.

Problem 16.3 Sketch the graph of the function and find its range.

1. $f\left(x\right)=3^x$
2. $f\left(x\right)={\left(\frac{1}{3}\right)}^x$

Problem 16.4 Use the given function to compare the values of $f(-1.05)$, $f\left(0\right)$ and $f\left(2.4\right)$ and determine which value is the largest and which value is the smallest. Explain your answer.

1. $f\left(x\right)={\left(\frac{5}{2}\right)}^x$
2. $f\left(x\right)={\left(\frac{2}{3}\right)}^x$